Спадило.ру

Решения

1. Масляная краска снизила коэффициент трения между колёсами и рельсами, что привело к пробуксовке, поезд не смог двигаться вперёд. Посыпав рельсы сажей, удалось решить проблему, так как коэффициент трения увеличился, и колёса перестали буксовать.
2. Санки находятся в движении, следовательно, на них будет действовать сила трения скольжения, численно равная Fтр. = μ ⋅ N, где N — сила реакции опоры, которая, при условии горизонтальной поверхности, равняется весу санок с мальчиком: N = m ⋅ g.  Получаем формулу Fтр. = μ ⋅ m ⋅ g  , откуда выразим искомую величину 

Ответ задачи зависит от того, сдвинется ли брусок под действием внешнего воздействия. Поэтому вначале узнаем значение силы, которую нужно приложить к бруску для скольжения. Это будет максимально возможная сила трения покоя, определяющаяся по формуле Fтр. = μ ⋅ N , где N = m ⋅ g (при условии горизонтальной поверхности). Подставляя значения, получаем, что Fтр. = 35 Н. Данное значение больше прикладываемой силы, следовательно брусок не сдвинется с места. Тогда сила трения покоя будет равна внешней силе: Fтр. = F = 25 H .

Движение тела, брошенного вертикально вверх

Движение тела, брошенного вертикально вверх, описывается в два этапа

Если известна скорость в момент времени t, для определения перемещения используется следующая формула:

Если время движения неизвестно, для определения перемещения используется следующая формула:

Формула определения скорости:

Какой знак выбрать — «+» или «–» — вам помогут правила:

• Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
• Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.

Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h₂ > h₁). По этой же причине время второго этапов движения тоже будет больше (t₂ > t₁). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v₂ > v₀₁).

Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.

Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:

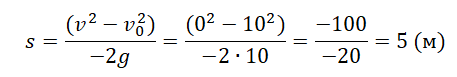
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).

Суммарное сопротивление

Является суммой всех видов сил сопротивления:

F=F+Fi{\displaystyle F=F_{0}+F_{i}}

Так как сопротивление при нулевой подъёмной силе F{\displaystyle F_{0}} пропорционально квадрату скорости, а индуктивное Fi{\displaystyle F_{i}} — обратно пропорционально квадрату скорости, то они вносят разный вклад при разных скоростях. С ростом скорости F{\displaystyle F_{0}} растёт, а Fi{\displaystyle F_{i}} — падает, и график зависимости суммарного сопротивления F{\displaystyle F} от скорости («кривая потребной тяги») имеет минимум в точке пересечения кривых F{\displaystyle F_{0}} и Fi{\displaystyle F_{i}}, при которой обе силы сопротивления равны по величине. При этой скорости самолёт обладает наименьшим сопротивлением при заданной подъёмной силе (равной весу), а значит, наивысшим аэродинамическим качеством.

Мощность, требуемая для преодоления силы паразитного сопротивления, пропорциональна кубу скорости, а мощность, требуемая для преодоления индуктивного сопротивления, обратно пропорциональна скорости, поэтому суммарная мощность тоже имеет нелинейную зависимость от скорости. При некоторой скорости мощность (а значит, и расход топлива) становится минимальной — это скорость наибольшей продолжительности полёта (барражирования). Скорость, при которой достигается минимум отношения мощности (расхода топлива) к скорости полёта, является скоростью максимальной дальности полёта или крейсерской скоростью.

Сопротивление при нулевой подъёмной силе

Эта составляющая сопротивления не зависит от величины создаваемой подъёмной силы и складывается из профильного сопротивления крыла, сопротивления элементов конструкции самолёта, не вносящих вклад в подъёмную силу, и волнового сопротивления. Последнее является существенным при движении с около- и сверхзвуковой скоростью, и вызвано образованием ударной волны, уносящей значительную долю энергии движения. Волновое сопротивление возникает при достижении самолётом скорости, соответствующей критическому числу Маха, когда часть потока, обтекающего крыло самолёта, приобретает сверхзвуковую скорость. Критическое число М тем больше, чем больше угол стреловидности крыла, чем более заострена передняя кромка крыла и чем оно тоньше.

Сила сопротивления направлена против скорости движения, её величина пропорциональна характерной площади S, плотности среды ρ и квадрату скорости V:

F=CFρv22S{\displaystyle F=C_{F}{\frac {\rho v^{2}}{2}}S}

CF{\displaystyle C_{F}} — безразмерный аэродинамический коэффициент сопротивления, получается из критериев подобия, например, чисел Рейнольдса и Фруда в аэродинамике.

Определение характерной площади зависит от формы тела:

• в простейшем случае (шар) — площадь поперечного сечения;
• для крыльев и оперения — площадь крыла/оперения в плане;
• для пропеллеров и несущих винтов вертолётов — либо площадь лопастей, либо ометаемая площадь винта;
• для подводных объектов обтекаемой формы — площадь смачиваемой поверхности;
• для продолговатых тел вращения, ориентированных вдоль потока (фюзеляж, оболочка дирижабля) — приведённая волюметрическая площадь, равная V2/3, где V — объём тела.

Мощность, требуемая для преодоления данной составляющей силы лобового сопротивления, пропорциональна кубу скорости (P=F⋅V=CFρV32S{\displaystyle P=F\cdot V=C_{F}{\dfrac {\rho V^{3}}{2}}S}).

Индуктивное сопротивление в аэродинамике

Индуктивное сопротивление (англ. lift-induced drag) — это следствие образования подъёмной силы на крыле конечного размаха. Несимметричное обтекание крыла приводит к тому, что поток воздуха сбегает с крыла под углом к набегающему на крыло потоку (т. н. скос потока). Таким образом, во время движения крыла происходит постоянное ускорение массы набегающего воздуха в направлении, перпендикулярном направлению полёта, и направленном вниз. Это ускорение, во-первых, сопровождается образованием подъёмной силы, а во-вторых — приводит к необходимости сообщать ускоряющемуся потоку кинетическую энергию. Количество кинетической энергии, необходимое для сообщения потоку скорости, перпендикулярной направлению полёта, и будет определять величину индуктивного сопротивления. На величину индуктивного сопротивления оказывает влияние не только величина подъёмной силы (так, в случае отрицательной работы подъёмной силы направление вектора индуктивного сопротивления противоположно вектору силы, обусловленной тангенсальным трением), но и её распределение по размаху крыла. Минимальное значение индуктивного сопротивления достигается при эллиптическом распределении подъёмной силы по размаху.
При проектировании крыла этого добиваются следующими методами:

• выбором рациональной формы крыла в плане;
• применением геометрической и аэродинамической крутки;
• установкой вспомогательных поверхностей — вертикальных законцовок крыла.

Индуктивное сопротивление пропорционально квадрату подъёмной силы Y, и обратно пропорционально площади крыла S, его удлинению λ{\displaystyle \lambda }, плотности среды ρ и квадрату скорости V:

Fi=CFiρV22S=Cy2πλρV22S=1πλY2ρV22S{\displaystyle F_{i}=C_{F_{i}}{\frac {\rho V^{2}}{2}}S={\frac {C_{y}^{2}}{\pi \lambda }}{\frac {\rho V^{2}}{2}}S={\frac {1}{\pi \lambda }}{\frac {Y^{2}}{{\frac {\rho V^{2}}{2}}S}}}

Таким образом, индуктивное сопротивление вносит существенный вклад при полёте на малой скорости (и, как следствие, на больших углах атаки). Оно также увеличивается при увеличении веса самолёта.

Уравнение координаты и скорости при свободном падении

Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:

Уравнение скорости при свободном падении:

v_y = v_0y + g_yt

Полезные факты

• В момент падения тела на землю y = 0.
• В момент броска тела от земли y = 0.
• Когда тело падает без начальной скорости (свободно) v = 0.
• Когда тело достигает наибольшей высоты v = 0.

Построение чертежа

Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.

План построения чертежа

• Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
• Отмечаются начальная и конечная координаты тела (y и y).
• Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.

Уравнение скорости:

–v = v – gt_пад

Уравнение координаты:

–v = v – gt

Уравнение координаты:

Тело подбросили от земли, на одной и той же высоте оно побывало дважды

Чертеж:

Интервал времени между моментами прохождения высоты h:

∆t = t₂ – t₁

Уравнение координаты для первого прохождения h:

Уравнение координаты для второго прохождения h:

Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ. Пример №5

Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?

Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?

Из условия задачи начальная скорость равна 0, а начальная координата — 50.

Поэтому:

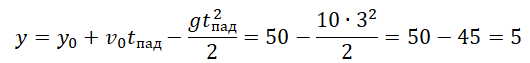
Через 3 с после падения тело окажется на высоте 5 м.

Индуктивное сопротивление в аэродинамике

Индуктивное сопротивление (англ. lift-induced drag) — это следствие образования подъёмной силы на крыле конечного размаха. Несимметричное обтекание крыла приводит к тому, что поток воздуха сбегает с крыла под углом к набегающему на крыло потоку (т. н. скос потока). Таким образом, во время движения крыла происходит постоянное ускорение массы набегающего воздуха в направлении, перпендикулярном направлению полёта, и направленном вниз. Это ускорение, во-первых, сопровождается образованием подъёмной силы, а во-вторых — приводит к необходимости сообщать ускоряющемуся потоку кинетическую энергию. Количество кинетической энергии, необходимое для сообщения потоку скорости, перпендикулярной направлению полёта, и будет определять величину индуктивного сопротивления. На величину индуктивного сопротивления оказывает влияние не только величина подъёмной силы (так, в случае отрицательной работы подъёмной силы направление вектора индуктивного сопротивления противоположно вектору силы, обусловленной тангенсальным трением), но и её распределение по размаху крыла. Минимальное значение индуктивного сопротивления достигается при эллиптическом распределении подъёмной силы по размаху.
При проектировании крыла этого добиваются следующими методами:

• выбором рациональной формы крыла в плане;
• применением геометрической и аэродинамической крутки;
• установкой вспомогательных поверхностей — вертикальных законцовок крыла.

Индуктивное сопротивление пропорционально квадрату подъёмной силы Y, и обратно пропорционально площади крыла S, его удлинению λ{\displaystyle \lambda }, плотности среды ρ и квадрату скорости V:

Fi=CFiρV22S=Cy2πλρV22S=1πλY2ρV22S{\displaystyle F_{i}=C_{F_{i}}{\frac {\rho V^{2}}{2}}S={\frac {C_{y}^{2}}{\pi \lambda }}{\frac {\rho V^{2}}{2}}S={\frac {1}{\pi \lambda }}{\frac {Y^{2}}{{\frac {\rho V^{2}}{2}}S}}}

Таким образом, индуктивное сопротивление вносит существенный вклад при полёте на малой скорости (и, как следствие, на больших углах атаки). Оно также увеличивается при увеличении веса самолёта.

Ссылки

• «Улучшенная эмпирическая модель для прогнозирования базового сопротивления ракетных конфигураций на основе новых данных о аэродинамической трубе», Франк Дж. Мур и др. НАСА Лэнгли Центр
• «Вычислительное исследование базового снижения лобового сопротивления снаряда при различных режимах полета», М.А. Сулиман и др. Материалы 13-й Международной конференции по аэрокосмическим наукам и авиационным технологиям, ASAT-13, 26 — 28 мая 2009 г.
• ‘Base Drag and Thick Trailing Edges’, Зигард Ф. Хёрнер, Air Materiel Command, в: Journal of the Aeronautical Sciences, октябрь 1950, стр. 622-628.

3.13. Силовой баланс автомобиля

Представим
уравнение движения автомобиля в следующем
виде:

(3.21)

В такой форме оно
называется уравнением силового баланса
автомобиля и выражает соотношение между
тяговой силой на ве­дущих колесах и
силами сопротивления движению.

На основании
уравнения (3.21) строится график силового
ба­ланса, позволяющий оценивать
тягово-скоростные свойства ав­томобиля.

При
построении графика силового баланса
(рис. 3.22) сначала строят тяговую
характеристику автомобиля. Затем наносят
зави­симость силы сопротивления
дороги от скорости. Если коэффи­циент
сопротивления дороги — постоянная
величина, то указан­ная зависимость
представляет собой прямую линию,
параллель­ную оси абсцисс, а при
непостоянном коэффициенте сопротив­ления
дороги — кривую параболической формы.
После этого от кривой, характеризующей
силу сопротивления дороги, отклады­вают
вверх значения силы сопротивления
воздуха при различных скоростях движения.
Полученная зависимость

Скорости движения (а), давления воздуха в шине (б) и момента, передаваемого через колесо (в)

факторов
и определяется экспериментально. Его
средние значения для различных дорог
при нормальном давлении воздуха в шине
составляют 0,01 …0,1.Рассмотрим влияние
различных факторов на коэффициент
сопротивления качению.

Скорость
движения.
При изменении скорости движения в
ин­тервале 0…50 км/ч коэффициент
сопротивления качению изме­няется
незначительно и его можно считать
постоянным в указан­ном диапазоне
скоростей.

При
повышении скорости движения за пределами
указанного интервала коэффициент
сопротивления качению существенно
уве­личивается (рис. 3.15, а)
вследствие
возрастания потерь энергии в шине на
трение.

Коэффициент
сопротивления качению в зависимости
от ско­рости движения можно приближенно
рассчитать по
формуле

где
—
скорость
автомобиля, км/ч.

Тип
и состояние покрытия дороги.
На дорогах с твердым по­крытием
сопротивление качению обусловлено
главным образом деформациями шины.

При
увеличении числа дорожных неровностей
коэффициент сопротивления качению
возрастает.

На
деформируемых дорогах коэффициент
сопротивления ка­чению определяется
деформациями шины и дороги. В этом случае
он зависит не только от типа шины, но и
от глубины образую­щейся колеи и
состояния грунта.

Значения
коэффициента сопротивления качению
при рекомен­дуемых уровнях давления
воздуха и нагрузки на шину и средней
скорости движения на различных дорогах
приведены ниже:

Асфальто-
и цементобетонное шоссе:

в
хорошем состоянии
………………………………. 0,007…0,015

в
удовлетворительном состоянии
…………… 0,015…0,02

Гравийная
дорога в хорошем состоянии …. 0,02…0,025

Булыжная
дорога в хорошем состоянии…… 0,025…0,03

Грунтовая
дорога сухая, укатанная …………..
0,025…0,03

Песок…………………………………………………………..
0,1…0,3

Обледенелая
дорога, лед …………………………. 0,015…0,03

Укатанная
снежная дорога ………………………..
0,03…0,05

Тип
шины.
Коэффициент сопротивления качению во
многом зависит от рисунка протектора,
его износа, конструкции каркаса и
качества материала шины. Изношенность
протектора, уменьше­ние числа слоев
корда и улучшение качества материала
приводят к падению коэффициента
сопротивления качению вследствие
снижения потерь энергии в шине.

Давление
воздуха в шине.
На дорогах с твердым покрытием при
уменьшении давления воздуха в шине
коэффициент сопро­тивления качению
повышается (рис. 3.15, б).
На
деформируемых дорогах при снижении
давления воздуха в шине уменьшается
глу­бина колеи, но возрастают потери
на внутреннее трение в шине. Поэтому
для каждого типа дороги рекомендуется
определенное давление воздуха в шине,
при котором коэффициент сопротивле­ния
качению имеет минимальное значение.

Нагрузка
на колесо.
При увеличении вертикальной нагрузки
на колесо коэффициент сопротивления
качению существенно возрастает на
деформируемых дорогах и незначительно
— на до­рогах с твердым покрытием.

Момент,
передаваемый через колесо.
При передаче момента через колесо
коэффициент сопротивления качению
возрастает (рис. 3.15, в)
вследствие
потерь на проскальзывание шины в месте
ее контакта с дорогой. Для ведущих колес
значение коэффициента сопротивления
качению на 10… 15 % больше, чем для ведомых.

Коэффициент
сопротивления качению оказывает
существен­ное влияние на расход
топлива и, следовательно, на топливную
экономичность автомобиля. Исследования
показали, что даже не­большое уменьшение
этого коэффициента обеспечивает
ощути­мую экономию топлива. Поэтому
неслучайно стремление конст­рукторов
и исследователей создать такие шины,
при использова­нии которых коэффициент
сопротивления качению будет незна­чительным,
но это весьма сложная проблема.

Типы

Типы перетаскивания обычно делятся на следующие категории:

• паразитическое сопротивление , состоящее из
  • ,
  • ,
• сопротивление , вызванное подъемной силой , и
• волновое сопротивление ( аэродинамика ) или волновое сопротивление (гидродинамика корабля).

Выражение « паразитное сопротивление» в основном используется в аэродинамике, поскольку для подъема крыльев сопротивление обычно мало по сравнению с подъемной силой. Для обтекания обтекаемых тел преобладают сопротивление формы и трение кожи, и тогда определение «паразитический» не имеет смысла.

Базовое сопротивление ( аэродинамическое ) сопротивление, создаваемое объектом, движущимся через жидкость, за счет формы его заднего конца.

Кроме того, сопротивление, вызываемое подъемной силой, имеет значение только при наличии крыльев или подъемного тела , и поэтому обычно обсуждается либо в авиации, либо при проектировании полу глиссирующего или глиссирующего корпуса . Волновое сопротивление возникает, когда твердый объект движется в газе со скоростью звука или близкой к ней, или когда твердый объект движется вдоль границы жидкости, как в случае поверхностных волн .

Коэффициент сопротивления C _d для сферы как функция числа Рейнольдса Re , полученный в результате лабораторных экспериментов. Темная линия соответствует сфере с гладкой поверхностью, а более светлая линия соответствует шероховатой поверхности.

Перетаскивание зависит от свойств жидкости, а также от размера, формы и скорости объекта. Один из способов выразить это с помощью уравнения сопротивления :

FDзнак равно12ρv2CDА{\ Displaystyle F_ {D} \, = \, {\ tfrac {1} {2}} \, \ rho \, v ^ {2} \, C_ {D} \, A}

где

FD{\ displaystyle F_ {D}}является силой сопротивления ,

ρ{\ displaystyle \ rho}- плотность жидкости,

v{\ displaystyle v} — скорость объекта относительно жидкости,

А{\ displaystyle A}— площадь поперечного сечения , а

CD{\ displaystyle C_ {D}}— коэффициент лобового сопротивления — безразмерное число .

Коэффициент лобового сопротивления зависит от формы объекта и числа Рейнольдса.

резнак равноvDνзнак равноρvDμ{\ displaystyle R_ {e} = {\ frac {vD} {\ nu}} = {\ frac {\ rho vD} {\ mu}}},

где

D{\ displaystyle D}— некоторый характерный диаметр или линейный размер . Фактически это эквивалентный диаметр объекта. Ведь сфера — это D самой сферы.D{\ displaystyle D}Dе{\ displaystyle D_ {e}}Dе{\ displaystyle D_ {e}}

Для поперечного сечения прямоугольной формы в направлении движения,, где a и b — края прямоугольника.Dезнак равно1,30⋅(а+б)0,625(а+б)0,25{\ displaystyle D_ {e} = 1.30 \ cdot {\ frac {(a + b) ^ {0.625}} {(a + b) ^ {0.25}}}}

ν{\ displaystyle {\ nu}}- кинематическая вязкость жидкости (равная динамической вязкости, деленной на плотность ).μ{\ displaystyle {\ mu}}ρ{\ displaystyle {\ rho}}

При низких , асимптотически пропорционально , что означает , что сопротивление линейно пропорциональна скорости. При высоких , более или менее постоянным и сопротивление будет изменяться пропорционально квадрату скорости. График справа показывает, как меняется с для случая сферы. Поскольку мощность, необходимая для преодоления силы сопротивления, является произведением силы на скорость, мощность, необходимая для преодоления сопротивления, будет изменяться как квадрат скорости при малых числах Рейнольдса и как куб скорости при больших числах.
ре{\ displaystyle R_ {e}}CD{\ displaystyle C_ {D}}ре-1{\ displaystyle R_ {e} ^ {- 1}}ре{\ displaystyle R_ {e}}CD{\ displaystyle C_ {D}}CD{\ displaystyle C_ {D}}ре{\ displaystyle R_ {e}}

Можно продемонстрировать, что сила сопротивления может быть выражена как функция безразмерного числа, которое по своим размерам идентично числу Бежана. Следовательно, сила сопротивления и коэффициент сопротивления могут быть функцией числа Беджана. Фактически, из выражения силы сопротивления было получено:

Dзнак равноΔпАшзнак равно12CDАжνμл2реL2{\ displaystyle D = \ Delta _ {p} A_ {w} = {\ frac {1} {2}} C_ {D} A_ {f} {\ frac {\ nu \ mu} {l ^ {2}} } Re_ {L} ^ {2}}

и, следовательно, позволяет выразить коэффициент лобового сопротивления как функцию числа Бежана и отношения между влажной площадью и передней площадью :
CD{\ displaystyle C_ {D}}Аш{\ displaystyle A_ {w}}Аж{\ displaystyle A_ {f}}

CDзнак равно2АшАжBереL2{\ displaystyle C_ {D} = 2 {\ frac {A_ {w}} {A_ {f}}} {\ frac {Be} {Re_ {L} ^ {2}}}}

где — число Рейнольдса, связанное с длиной пути жидкости L.
реL{\ displaystyle Re_ {L}}

Свободное падение

Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:

Скорость

v = gt

v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело

Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.

Подставляем данные в формулу и вычисляем:

v = gt = 10∙3 = 30 (м/с).

Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.

Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения. Высота падения

Высота падения

Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.

Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:

Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:

Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.

Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:

Формула определения перемещения тела в n-ную секунду свободного падения:

s(n) — перемещение за секунду n.

Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.

Примеры решения задач

ПРИМЕР 1

Задание

Максимальная скорость автомобиля на горизонтальном участке дороги равна при максимальной мощности его равной P. Коэффициент лобового сопротивления автомобиля C, а наибольшая площадь сечения в направлении, перпендикулярном скорости S. Автомобиль подвергся реконструкции, наибольшую площадь сечения в направлении, перпендикулярном скорости уменьшили до величины , оставив коэффициент сопротивления без изменения. Считайте силу трения о поверхность дороги неизменной, найдите какова максимальная мощность автомобиля, если его скорость на горизонтальном участке дороги стала равна

Плотность воздуха равна .

Решение

Сделаем рисунок.

Мощность автомобиля определим как:
где — сила тяги автомобиля.
Считая, что автомобиль на горизонтальном участке дороги движется с постоянной скоростью, запишем второй закон Ньютона в виде:
В проекции на ось X (рис.1), имеем:
Силу сопротивления, которую испытывает автомобиль, двигаясь в воздухе, выразим как:

Тогда мощность автомобиля можно записать:

Выразим из (1.5) силу трения автомобиля о дорогу:

Запишем выражение для мощности, но с изменёнными по условию задачи параметрами автомобиля:

Учтем, что сила трения автомобиля о дорогу не изменилась, и примем во внимание выражение (1.6):

Ответ

ПРИМЕР 2

Задание	Какова максимальная скорость шарика, который свободно падает в воздухе, если известны: плотность шарика (), плотность воздуха (), масса шарика (), коэффициент сопротивления C?
Решение	Сделаем рисунок. Запишем второй закон Ньютона для свободного падения шарика:

При движении любого предмета по поверхности или в воздухе возникают силы, препятствующие этому. Их называют силами сопротивления или трения. В этой статье мы расскажем, как найти силу сопротивления, и рассмотрим факторы, влияющие на нее.

Сопротивление движения в воздухе используется во время прыжков с парашютом. В результате возникающего трения между куполом и воздухом скорость движения парашютиста снижается, что позволяет без ущерба для жизни заниматься парашютным спортом.

Для определения силы сопротивления
воздуха
создайте условия, при которых тело начнет под действием силы тяжести двигаться равномерно и прямолинейно. Рассчитайте значение силы тяжести, оно будет равно силе сопротивления воздуха. Если тело движется в воздухе, набирая скорость, сила его сопротивления находится при помощи законов Ньютона, также силу сопротивления воздуха можно найти из закона сохранения механической энергии и специальных аэродинамических формул.

Инструкция

Определение сопротивления воздуха равномерно падающему телу Измерьте массу тела с помощью весов. Сбросив его с некоторой высоты, добейтесь, чтобы оно двигалось равномерно. Умножьте массу тела в килограммах на ускорение свободного падения, (9,81 м/с²), результатом будет сила тяжести, действующая на тело. А поскольку оно движется равномерно и прямолинейно, сила тяжести будет равна силе сопротивления воздуха.
Определение сопротивления воздуха телу, набирающему скоростьОпределите массу тела с помощью весов. После того как тело начало двигаться, с помощью спидометра или радара измерьте его мгновенную начальную скорость. В конце участка измерьте его мгновенную конечную скорость. Скорости измеряйте в метрах в секунду. Если приборы измеряют ее в километрах в час, поделите значение на 3,6. Параллельно с помощью секундомера определите время, за которое происходило это изменение. Отняв от конечной скорости начальную и поделив результат на время, найдите ускорение, с которым движется тело. Затем найдите силу, которая заставляет тело изменять скорость. Если тело падает, то это сила тяжести, если тело движется горизонтально – сила тяги двигателя. От этой силы отнимите произведение массы тела на его ускорение (Fc=F+m a). Это и будет сила сопротивления воздуха

Важно, чтобы при движении тело не касалось земли, например, двигалось на воздушной подушке или падало вниз.
Определение сопротивления воздуха телу, падающему с высотыИзмерьте массу тела и сбросьте его с высоты, которая заранее известна. При контакте с поверхностью земли зафиксируйте скорость тела с помощью спидометра или радара

После этого найдите произведение ускорения свободного падения 9,81 м/с² на высоту, с которой падало тело, отнимите от этого значения скорость, возведенную в квадрат. Полученный результат умножьте на массу тела и поделите на высоту, с которой оно падало (Fc=m (9,81 H-v²)/H). Это и будет сила сопротивления воздуха.

Суммарное сопротивление

Является суммой всех видов сил сопротивления:

F=F+Fi{\displaystyle F=F_{0}+F_{i}}

Так как сопротивление при нулевой подъёмной силе F{\displaystyle F_{0}} пропорционально квадрату скорости, а индуктивное Fi{\displaystyle F_{i}} — обратно пропорционально квадрату скорости, то они вносят разный вклад при разных скоростях. С ростом скорости F{\displaystyle F_{0}} растёт, а Fi{\displaystyle F_{i}} — падает, и график зависимости суммарного сопротивления F{\displaystyle F} от скорости («кривая потребной тяги») имеет минимум в точке пересечения кривых F{\displaystyle F_{0}} и Fi{\displaystyle F_{i}}, при которой обе силы сопротивления равны по величине. При этой скорости самолёт обладает наименьшим сопротивлением при заданной подъёмной силе (равной весу), а значит, наивысшим аэродинамическим качеством.

Мощность, требуемая для преодоления силы паразитного сопротивления, пропорциональна кубу скорости, а мощность, требуемая для преодоления индуктивного сопротивления, обратно пропорциональна скорости, поэтому суммарная мощность тоже имеет нелинейную зависимость от скорости. При некоторой скорости мощность (а значит, и расход топлива) становится минимальной — это скорость наибольшей продолжительности полёта (барражирования). Скорость, при которой достигается минимум отношения мощности (расхода топлива) к скорости полёта, является скоростью максимальной дальности полёта или крейсерской скоростью.